Chemotherapy broadly refers to the use of anti-neoplastic drugs in different clinical settings, in the management of the major public health problem of cancer, without injuring the host cells. But the drugs which target the proliferating cells exert little selectivity on the proliferating normal tissues, resulting in significant toxicity with additional morbidity. So, the primary obstacles in the way of the clinical efficacy of chemotherapy, have been the toxicity to the normal tissues of the body and the development of cellular resistance to these agents, which minimise the therapeutic effects [1].
There are various strategies for overcoming these major pitfalls of cancer chemotherapy. A combination chemotherapy is based on the principle that drugs should be used in the optimal dose and schedule without any overlap in their toxicities and there should be a clear understanding of the biochemical, molecular and the pharmacokinetic mechanisms of the interaction between the individual drugs in a given combination, to allow a maximal effect [2,3]. In spite of these measures, a rational therapy with anticancer drugs, especially with the right doses for each patient, is still an uncertainty among physicians [4].
Most of the anticancer drugs have a narrow therapeutic range; hence, small changes in their doses can lead to either a therapeutic failure or an unacceptable toxicity [5]. The rationality of the routine methods for using the Body Surface Area (BSA) to dose the antineoplastic agents is being controversial now- a-days and an irrelevant correlation between this variable and the Pharmacokinetic (PK) parameters has been established for most of the drugs [6]. It is recommended that a safe but not a sub therapeutic dose is given to the patient initially and later, the biological end points are used for each patient to titrate the individual doses. Saving the sensitive normal tissue of a cancer patient is a real challenge in certain situations and it is highly dependable on the clinical expertise and the experience of the treating physicians [7]. Even though dose optimisation with the use of pharmacokinetic data, which is called therapeutic drug monitoring and non invasive pharmaco dynamic techniques are there, the universal practicability is a questionable issue [5]. Very little information is available on the relationship between the toxicity and the response [8].
The scientific computing of drug scheduling by optimisation before drug administration, is one strategy for solving the uncertainty in the invivo measures of the drug dosage scheduling [9]. In a majority of these strategies, the pharmacodynamic uncertainties are given more importance than the pharmacokinetic ones [10]. When the drug dosage schedule is made more optimal, the number of cancer cells can be brought to a minimum at the end of the therapy. This also minimises the emergence of resistant cancer cells. Since the dose is within tolerable limits, the toxic effects can also be minimised.
Subjects and Methods
In the present study, the optimal chemotherapy schedules were provided with the objective of minimising the number of the tumour cell populations at the end of an 84 day cycle. The Gompertzian model is the basic mathematical model for representing the tumour cell population [11]. The details of the model have been provided by Martin [12,13]. With the optimal drug dosage schedule, the number of cancer cells can be brought to a minimum at the end of the therapy. The drug concentration must be kept below some level throughout the treatment period and the cumulative or toxic effect of the drug must be kept below the maximum tolerated dose. So, the optimal control of the drug scheduling has the objective of minimising the number of cells which are subject to the constraint of the drug toxicity.
The Gompertian model is:
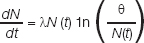
Where N is the number of Cancer cells. φ is the maximum carrying capacity of the tumour is the growth parameter =9.9 e-4/days
The optimization problem is formulated, so as to find the rate of the drug doses U= [u1,u2,u2,….un] such that the final cancer cell population is minimum. The objective function is formulated by using the Gompertian model and the drug scheduling. A transformation is used to make a model for optimization purposes, which is
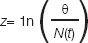
The objective function for the optimization problem is to maximize z (tf) (equivalent to minimize

The initial conditions and the constraints for the problem are
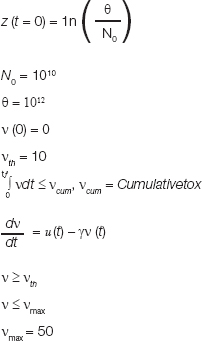
The performance index which has to be maximized is:
I=x1 (t1) where the final time tf = 84 days. The tumour size is constrained to reduce by at least 50% every 3 weeks [9,14,15], so that the constraints are
z (t = 21) ≥ 1n (200)
z (t = 42) ≥ 1n (400)
z (t = 63) ≥ 1n (800)
There is always an uncertainty in the invivo measures of the drug dosage scheduling, which is usually done in the Phase 1 and Phase 2 studies and in the clinical practice. This uncertainty can result in an ineffective range of the dose calculation, which later can be skewed to under dosing, toxicity and even resistance with the drugs. These problems during the dosage adjustment can be encountered by an optimal drug scheduling. Chemotherapy is generally given as cycles which involve a dose of one or more drugs, followed by a drug free interval, for the normal cells to recover. Some drugs are given continuously over a period of days. Considering this, different cases were analysed for this study.
Case one
The daily schedule from the 0–84th day continuously.
Case two
The daily schedule with φ
Case three
The drug is administered on days 0, 21, 42, 63 and 84 (21-day cycles)
Case four
The cyclic chemotherapy with φ.
Results
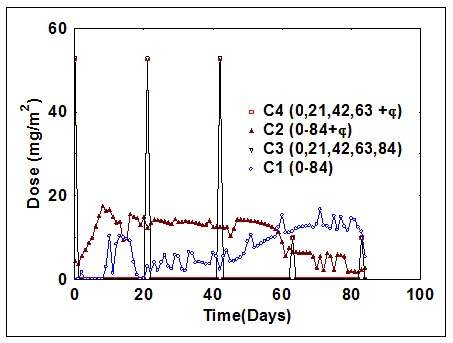
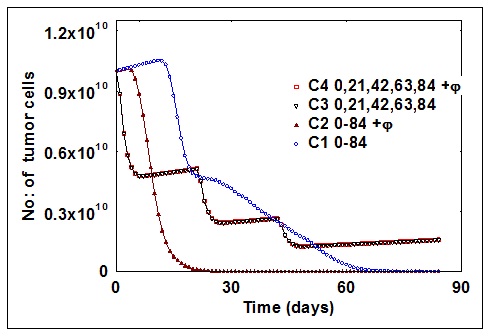
The optimal dose schedule during the treatment period, for 4 different cases, are given in [Table/Fig-1]. The number of tumour cells for those 4 cases have been depicted in [Table/Fig-2] and the cumulative toxicity that occurred during the treatment period has been depicted in [Table/Fig-3]. On analysing the dosage schedule, more dose is possible during the cyclic chemotherapy and the maximum dose in the first three cycles, with or without considering φ. The maximum tolerated dose by daily scheduling is almost doubled when φ is considered. The number of tumour cell killing denotes the performance index of the drug. The number of tumour cells killing with the daily drug treatment is (10.1) more than that in cyclic chemotherapy (6.5). When the φ factor is considered, there is no variation in the performance index with the cyclic chemotherapy, but it is more than doubled (23.6) with the daily dosing. Even with a 1 per cent effect, the maximum tumour cell killing with a reduced time line is possible.
Optimal dose schedule during the treatment period for four cases
Number of tumour cells for four cases
Cumulative toxicity occurred during the treatment period in four cases
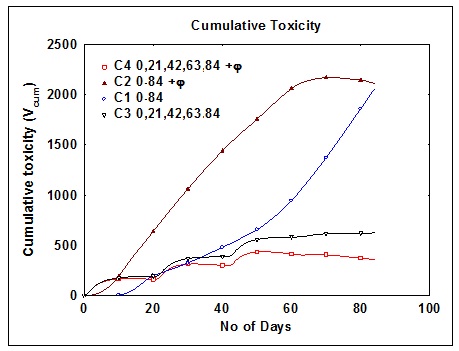
The cyclic chemotherapy which is commonly followed, has the disadvantage that the residual tumour cells which are resistant to the chemotherapy, remain. These can further undergo multiplication and growth, resulting in the formation of a tumour mass, which will not respond to that chemotherapy at all. The drug resistance cannot be minimised by the parameter, φ.The cumulative toxicity of the cyclic chemotherapy (628) is halved (365) when φ is considered. The cumulative toxicity seems to be increased (2110) when φ is considered in the daily dose (2055). But this increase is only marginal.
Discussion
In cancer chemotherapy, the maximum efficacious dose is as important as the selection of the right drug, because the optimal dose of the individual patients varies widely [4,5]. Each drug is given on a schedule that is carefully set up to make the most of its anti-cancer actions and to minimise the side effects. The tumour growth rate, along with the phase and the cell cycle specificity, depends on several interrelated factors like the normal cell cycle time, the growth fraction, the total number of cells in the population and the intrinsic cell death rate [16,17] and all these factors determine the sensitivity of the cancer cells to chemotherapy [16]. Chemotherapy is generally given as cycles which involve a dose of one or more drugs, followed by a drug free interval for the normal cells to recover. Some drugs are given continuously over a period of days [18]. Considering this, this study has analysed four cases.
The dose optimisation is usually done by measuring the biological end points and the pharmacokinetic data by therapeutic drug monitoring,undertaking pharmacodynamic studies which correlate with either their toxicity, efficacy, or both and by modifying the dose [19,20]. There are problems with the therapeutic drug monitoring in cancer chemotherapy. These include the inability to reach a steady state concentration, a need for the activation of prodrugs, the variation between the concentrations of the drugs in the plasma and tumour tissue drug interactions [21]. Mathematical modelling and computer simulation can be used as tools for better understanding the cancer chemotherapy [22].
In a study, the kinetics of the drug were considered, to formulate an optimal chemotherapy and it was determined that it has a role in the correlation between the drug concentration at the tumour site and the delivered drug concentration [23].
In another study, it was mentioned that even though a pharmacokinetic optimization was difficult, the role of the cytochrome p450 enzymes mediated a drug interaction which has a significant role in the cancer therapy 15. Various logistic and Gompertzian models have proved beyond doubt, the importance of the role of the renal excretion, especially filtration and passive reabsorption and its individual variations [24,25].
The treatment plan should specify as to how often and exactly when each drug should be given, based on the type and the stage of the cancer, the health status of the patient and the side effects. Scientific computing of the drug scheduling by optimization, before the drug administration, by considering the individual variation (φ) and an individualised dose, can be given in the first cycle. Later, fine tuning of the doses can be done, based on the toxicity and the other biological effects. These measures can further minimise the errors which are encountred in cancer chemotherapy.
Conclusion
Calculating the dosage requirement, based on the body surface area, then computing and titrating the dosage schedule, based merely on the biological end points, the efficacy and the toxicity, is not sufficient. Even before the drug administration, some model based calculations on the dosage should be done, considering the interindividual variations in pharmacokinetics and they should be given due importance.
The maximum possible dose and the performance index are increased in the daily scheduling, when the pharmacokinetic parameters (φ) are considered. But in cyclic therapy, even though the maximum tolerated dose or the performance index is not altered, the cumulative toxicity is greatly reduced. So, daily scheduling and cyclic chemotherapy can be applied alternatively in a more effective manner; if the individual variations in the pharmacokinetic factors are considered.