Historical Perspective
LEONARDO PISANO- 1170-1250
“The greatest European mathematician of the middle ages”,
Leonardo Pisano is one of the most renowned names in mathematics who was better known as Fibonacci. He was an Italian mathematician who was educated in North Africa where he learned Arabic mathematics. He was credited with number of important texts which played an imperative role in reviving ancient mathematical skills [1].
In the year 1202, Leonardo wrote a book called “Liber Abaci” (Book of Calculation), in which he strengthened the use of Hindu-Arabic numeral system describing its many benefits over the unwieldy system of Roman numerals then in use in Europe [2,3].
Fibonacci wrote another book, Practica geometriae in 1220 the book includes geometrical problems and theorems arranged in eight chapters which describes there precise proofs. It also includes practical information for surveyors.
Fibonacci is recognised for his pioneering discovery of a particular number sequence, which has since become known as Fibonacci Numbers or the Fibonacci Sequence [2].
Introduction
The Golden Proportion is known as mathematics of harmony since the ancient past. This is regarded as the blueprintfor topographies in nature, art, architecture and humans that adhere to the harmony and beauty. This proportion circumscribe both organic and inorganic entities and has been found in abundant natural and architectural marvels. Though its concept is easy to understand but its applications have been proved to be complex. Its simplicity is very perplexing. Fibonacci numbers and its derivations is known by various names- Golden number, Divine proportion, Golden ratio, Golden proportion, Nature’s numbering system.
The Rabbit Problem (Fibonacci Numbers)
The third section of book “Liber abaci” written by Fibonacci in the year 1202 describes an inquisitive problem, which is now generally denoted as “The Rabbit Problem”. This problem led to the introduction of the Fibonacci numbers and the Fibonacci sequence for which Fibonacci is best remembered today.
As explained in [Table/Fig-1], Fibonacci hypothesised the breeding process of rabbits.
Fibonacci numbers in breeding process of rabbits.

It continues every month and each rabbit pair produces a mixed pair of baby rabbits who mature the next month.
Number of rabbits in a month is equal to the total pairs in the previous month.
In mathematical terms this sequence could extend indefinitely.
The Fibonacci sequence is 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and so on [4].
There is another series quite similar to the Fibonacci series that often occurs when working with the Fibonacci series. Edouard Lucas (1842-1891) (who gave the name “Fibonacci Numbers” to the series written about by Leonardo of Pisa) studied this second series of numbers: 2, 1, 3, 4, 7, 11, 18,.. called it the Lucas numbers in his honour [5].
Each number in the sequence is the sum of 2 numbers that precede it [Table/Fig-2]. The mathmatical equation describing this is given below [6]:
| 2÷1 | 2.000 |
| 3÷2 | 1.5 |
| 5÷3 | 1.666 |
| 8÷5 | 1.600 |
| 13÷8 | 1.6250 |
| 21÷13 | 1.6154 |
| 34÷21 | 1.6190 |
| 55÷34 | 1.6176 |
| 89÷55 | 1.6182 |
Xn+2=Xn+1+XnIt is imperative to understand the difference Fibonacci sequence and golden ratio. The golden ratio is derived from fibonacci numbers.
Derivation of Phi ϕ =1.618 (The golden ratio)
The Phidias, a famous Greek sculptor and mathematician used the Golden Proportion in his architecture so much that it came to be known as phi. The Golden Proportion, a mathematical ratio, epitomises beauty, congruence and balance in physical form. It is derived by expressing ratio using a line segment where the ratio of the whole segment to the longer segment is equal to the ratio of the longer segment to the shorter segment as depicted in [Table/Fig-3]. Mathematically, the precise value of this ratio is expressed as 1.6180339887..., an interminable number which goes to infinity.
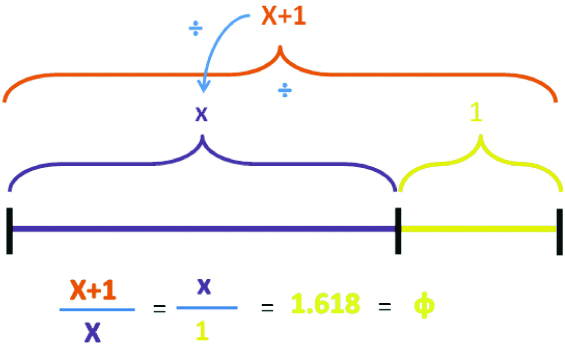
Unravelling Golden Spiral and Golden Rectangle
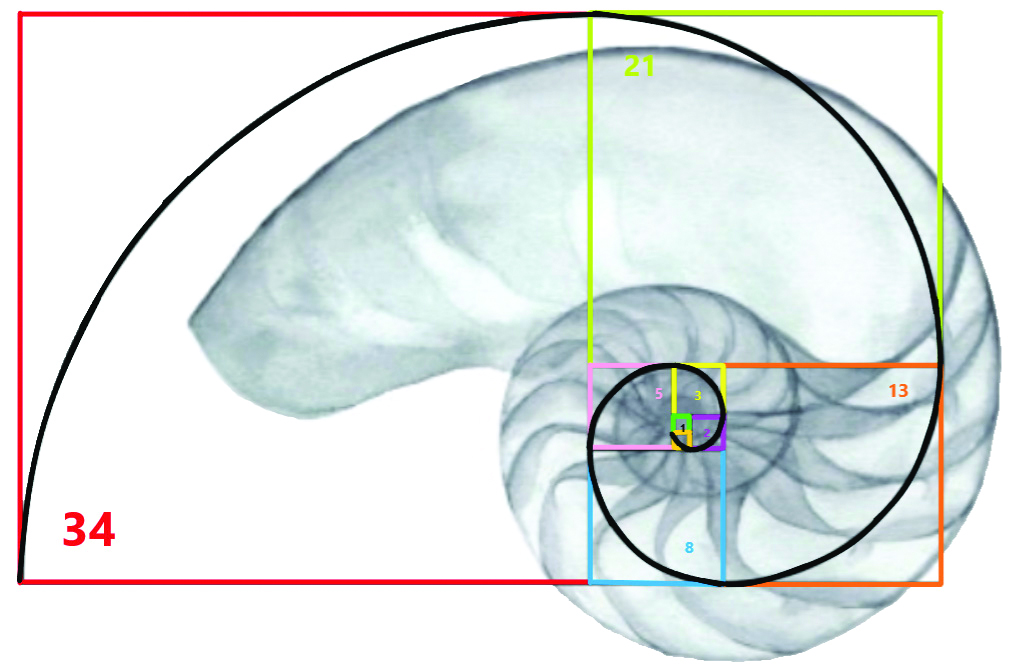
The most archetypal symbol of the Golden Ratio is a nautilus shell. The beautifully designed spiral exhibits nature’s exemplary display. The conformation of nautilus shell was golden spiral based upon the Golden Ratio and derived from a Golden Rectangle .A rectangle with sides in the ratio of 1: ϕ is known as a Golden Rectangle [2]. In order to construct it, one should begin with two squares (one arbitrary unit) adjacent to one another. Then another square is drawn touching both the existing squares (two arbitrary units). Then a third arbitrary unit is drawn touching all the squares. Five arbitrary units, should be added, contacting the one-arbitrary unit original square, as well as the three-arbitrary unit square as illustrated in [Table/Fig-4a].
Formation of arbitrary squares.

To add a descriptive diagram here. This process with squares of increasing Fibonacci units is continued which will result in the creation of the Golden Rectangle. To create the Golden Spiral, the corners of the squares should be joined in a spiral-shape. The spiral escalates outward by a growth rate of 1.618 for each quarter-turn which should not end discretly but continue indefinitely [Table/Fig-4b] [7].
Nautilus shell and golden rectangle.
Golden Proportion Calipers
To conform to the validity of the impressive golden proportion, the golden proportion calipers were established for prompt and easy analysis. The calipers always open to the persistent ratio between larger and smaller fraction. Its points are in a fixed proportion at any opening [8]. Illustrative example is hown in [Table/Fig-5a,b].
Golden proportion calipers showing the dominant color separation in bird (left) and flower (right).
Image Courtesy: The Golden Proportion, Beauty and Dental Aesthetics. Available from: https://goldenmeangauge.co.uk/applications/nature/

Applications
Plant Kingdom
Fibonacci sequence application can also be appreciated in plants. It has been observed that each flower has specific number of petals and a special arrangement [9]. For example the Daisy Oracle game of “He loves me/He loves me not” played by Wild daisy has 34 petals, blackeyed Susan and aster 21 petals, corn marigolds have 13 petals, delphiniums have eight petals, primroses, buttercups, wild roses have five petals, and lilies and irises contain three petals [7]. All these numbers are contained in the Fibonacci sequence i.e. is 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 and so on This organisation may be related to maximising the space and light for each leaf.
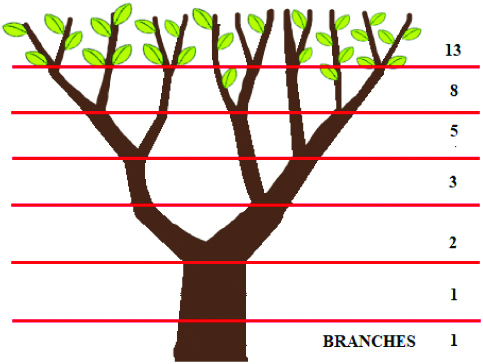
Botanists have also discovered phyllotaxis arrangement according to Fibonacci numbers. As shown in [Table/Fig-6], if a tree has one branch at the very beginning, it will have two branches after a year. In the next circle it has 3 branches. The numbers go upto in the fashion of 1,1,2,3,5,8,13 and so on. In a nutshell, every year the total branches of the tree composed a Fibonacci sequence [10].
Fibonacci sequence in branching pattern of trees.
The Phi Concept in Arrangement of Seeds
The concept of Phi can be applied to the growth pattern of seeds. The Golden Spiral Seed arrangement is promising as it makes maximum space for seeds that can be packed into the flower’s seed head. The placement of the new seed is relative to the position of the previous seed, for example
if a seed grows at an angle of 180° or 0.5 turns the consequential seed head would be two straight arms.
If it takes 0.6 turns there would be 5 arms of seeds arrangement.
On 0.7 turns, 10 arms of seeds would emerge [Table/Fig-7a].
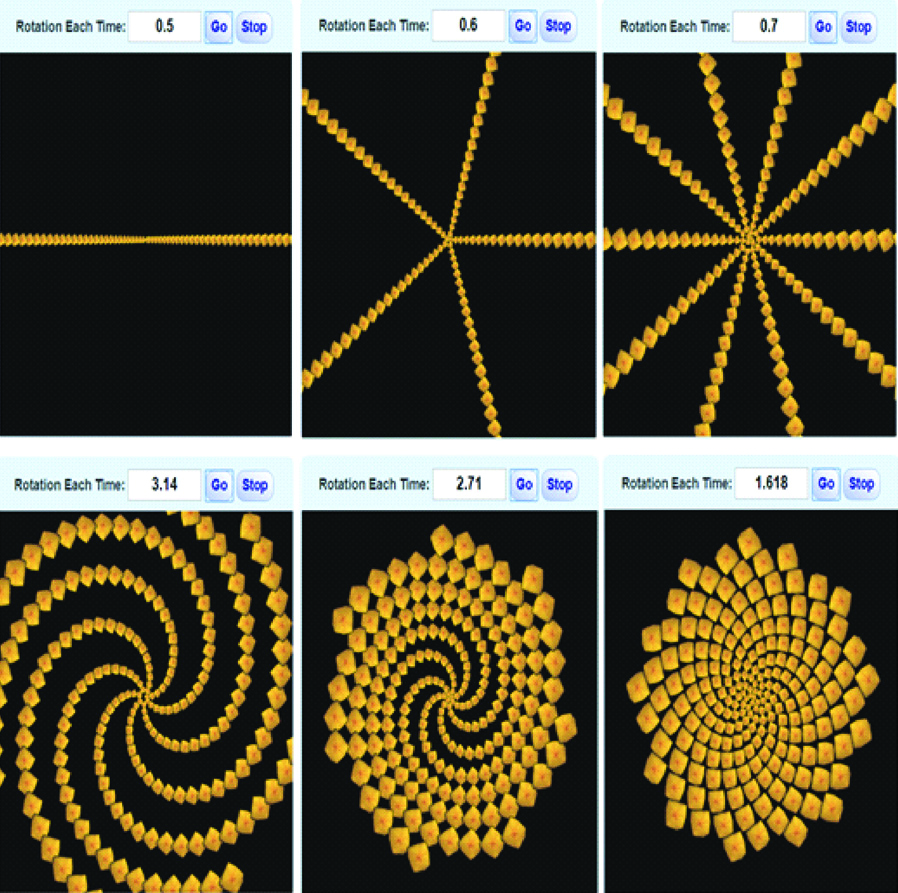
To entail a maximum number of seeds with little to no unused space, the numbers such as pi (p), Euler’s number or log to the base e (e) and phi (ϕ) were tried. [Table/Fig-7a] explains the seed arrangement with these irrational numbers. The value of Phi 1.618 makes a total turn of 1+0.618. To understand this, the golden angle is derived which is calculated by considering circumference of circle divided into two arms, long and short. The golden angle would be shorter of the two angles as shown in [Table/Fig-7b]. It is derived from an approximation of 0.168*360=222.5 i.e. 137.5° (360-222.5). which necessitates maximum number of seeds [7]. This way Phi would entail the maximum number of seeds in the seed head.
Derivation of Golden angle.
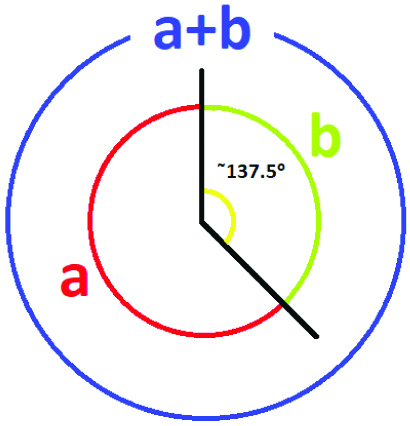
Any deviation either of only 1 degree will result in significant empty space in between [7].
Animal Kingdom
Bees
Fibonacci sequence also occur in real populations, here honeybees provide an example. A look at the pedigree of family tree of honey bee suggests that mating tendencies follow the Fibonacci numbers.
In a colony of honeybees there is one distinctive female called the queen. The other females are worker bees who, unlike the queen bee, produce no eggs. Male bees do no work and are called drone bees. When the queen lays eggs, the eggs could be either fertilised or unfertilised. The un fertilised eggs would result in drone (male bee) which carry 100% of their genome and fertilised eggs will result in female worker bees which carry 50% of their genome.
Males are produced by the queen’s unfertilised eggs, so male bees only have a mother but no father. All the females are produced when the queen has mated with a male and so have two parents. Females usually end up as worker bees but some are fed with a special substance called royal jelly which makes them grow into queens ready to go off to start a new colony when the bees form a swarm and leave their home (a hive) in search of a place to build a new nest.
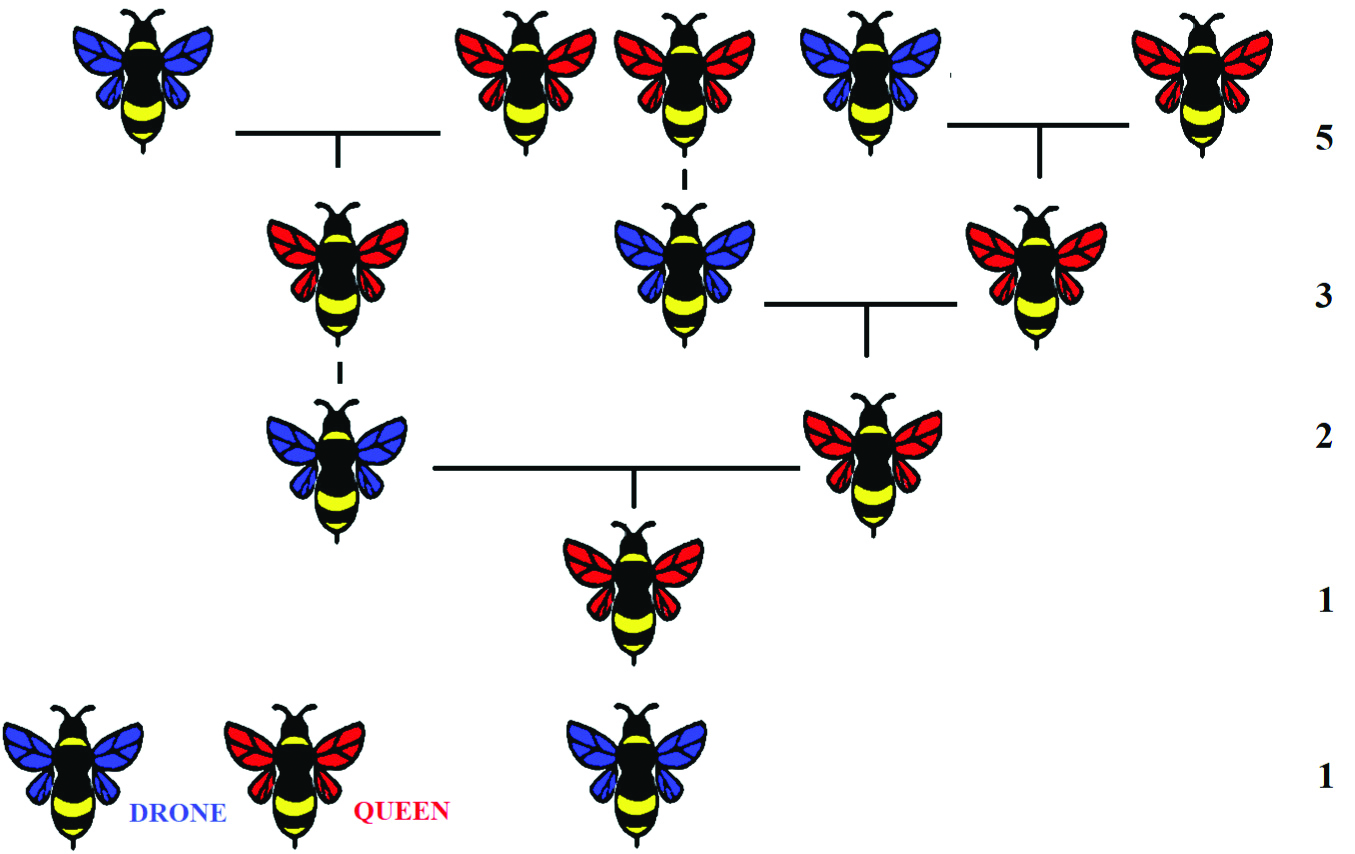
Remarkably, this means that the family tree of a single male bee if followed back several generations results in a Fibonacci sequence of the number of individuals in each generation (1, 1, 2, 3, 5...) [Table/Fig-8] [11].
DNA
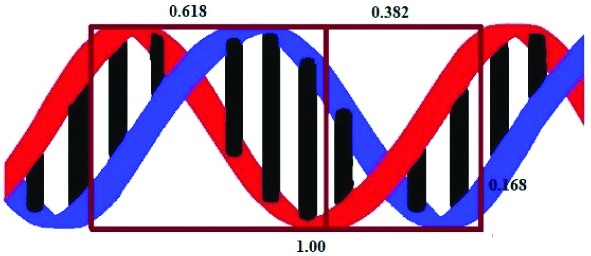
The basic structure of life i.e the DNA also contains Golden Proportion in its structure. The double helix cross section of the DNA forms a golden decagon. It is constituted by two pentagons rotated at as angle by 36 degrees having diagonal ratio of 1:1.68. The ratio of length by width of the DNA molecule (34 Å long by 21 Å) for each full cycle of the double helix shape makes a ratio of 1.619 (ratio 34/21 equals 1.619…) as show in [Table/Fig-9] [8]. The ratio of the major to the minor groove (21 angstroms to 13 angstroms) in DNA is also golden (21/13 equals 1.619).
Golden proportion in DNA.
Organs of The Human Body
Human Hand
Each finger in the human hand has three parts called the phalanges. In the human hand, the length of bones is also in Fibonacci numbers [9].
According to Hamilton and Dunsmuir’s findings a series of 1x, 1.3x, 2.3x is observed in index, second, and third digits [12]. Additionally, they provided dimension data for the fourth digit (little finger) that follows the first initial values of a Fibonacci sequence of 0,1,1,2, represented by y, y, and 2y in [Table/Fig-10].
Fibonacci numbers in human hand.
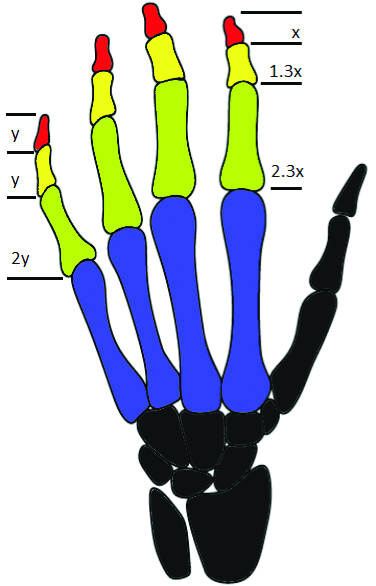
Therefore, additive rule of Lucas series is followed for index, second and third digits while approximating Fibonacci values for the fourth digit (little finger).
Heart
Henein MY et al., in their study observed golden ratio and golden angle measurements application in the absolute dimensions of the heart irrespective of ethnicity. They theorized that since the golden ratio and angle are so intensely entrenched in nature, they must have some correspondence in the healthy heart structure and function. In their study the left ventricles of 30 Chinese, along with 30 Swedish patients were measured via echocardiogram. The Chinese population tended to have less significant smaller measurements than the Swedish population; however, a evaluation between the vertical (~8 mm) and transverse (~5 mm) measurements yielded a Golden Ratio in both populations. They observed that the vertical and transverse dimensions follow the golden ratio. The angles between the outflow tract axis and inflow tract axis and angle between pulmonary trunk and ascending aorta approximated to the golden angle i.e.137.5 degree. This suggests that the overall ventricular and cardiac dimensions of a normal heart are in accordance with the golden ratio and angle [13]. Any deviation from normality could have anatomical, functional values and may act as prognostic indicator markers.
In a separate study, Yetkin et al. monitored the blood pressure, an indication of heart function, of 462 patients using an ambulatory blood pressure monitor. They found that, at night, the systolic to diastolic blood pressure ratio of patients approximated the Golden Ratio [14]. They hypothesized that the non existance of Golden Ratio during the day was due to an activated sympathetic nerves system’s influence on the heart, caused by daytime environmental stimuli and physical activity. On the contrary, at night, when patients are in a more relaxed state, the parasympathetic nervous system have a tendency control bodily function, causing the systolic/diastolic ratio to gravitate towards the Golden Ratio. According to Prasanth G, the cardiac performanc is subordinated to the Goldan section law [15]. The studies of human heart anatomy and function correlated best with the golden ratio and good health, but the implications have yet to be defined. Further studies should be undertaken to incorporate golden ratio in cardiac therapies.
Ear
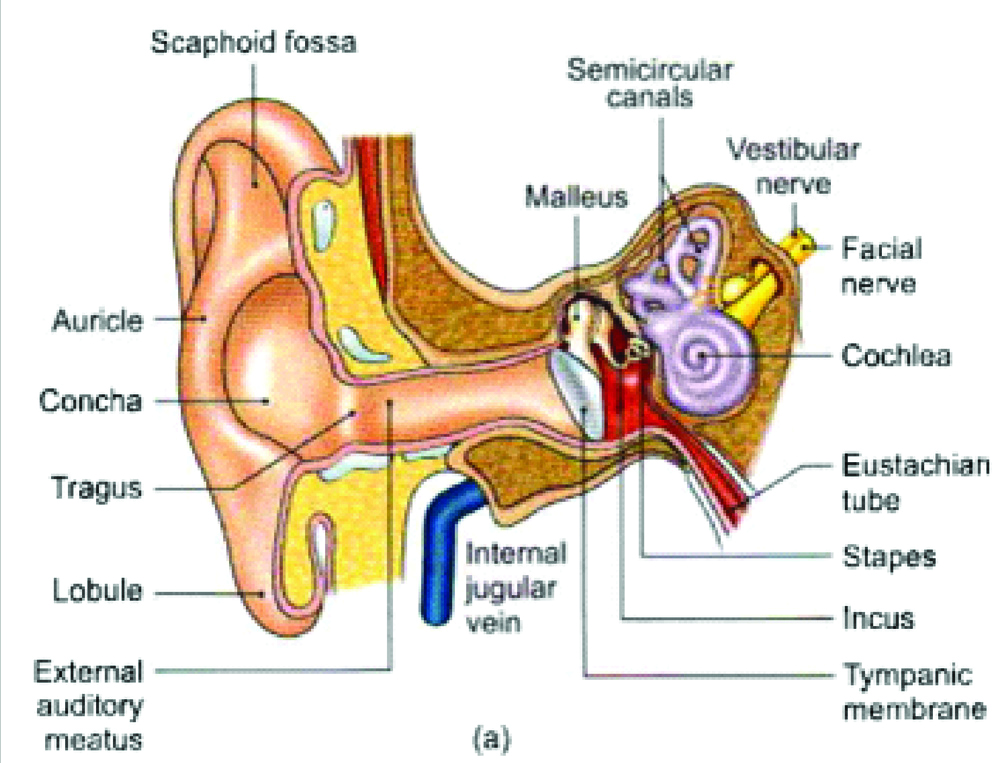
The Golden Ratio can also be observed in the hearing mechanism of humans specifically the spirals of pinna and spiral shaped cochlear bone. In humans pinna is spiral shaped which correspond to the the change in the perception of sound if the ears are either bend forwards or backwards.
Reasearch has shown, that over time the shape of cochlea in some mammals and marsupials have evolved into spiral shape. Spiral shapes cochlear bones present in the inner ear are exclusive to mammals. Sound waves enter through the tympanum (14). Essentially, as the length of the cochlea increases, so does the range of sound that can be perceived due to a greater number of hair cells [Table/Fig-11] [7]. M. Pietsch et al. suggested that a longer cochlea can best supplement space within the constraints of a mammalian skull by conforming into a coil shape, most efficiently, a Golden Ratio spiral, alike the packing of a seed head in plants [16]. Although there were some drawbacks in the study which demands further research. It has been proposed that if the results of Golden ratio are substantiated then it can help in research for new areas such as Cochlear implants.
Golden spiral in pinna and cochlea.
Image Courtesy: BD Chaurasia’s Human Anatomy Regional and Applied Dissection and Clinical: Vol. 3: Head-Neck Brain
Lung
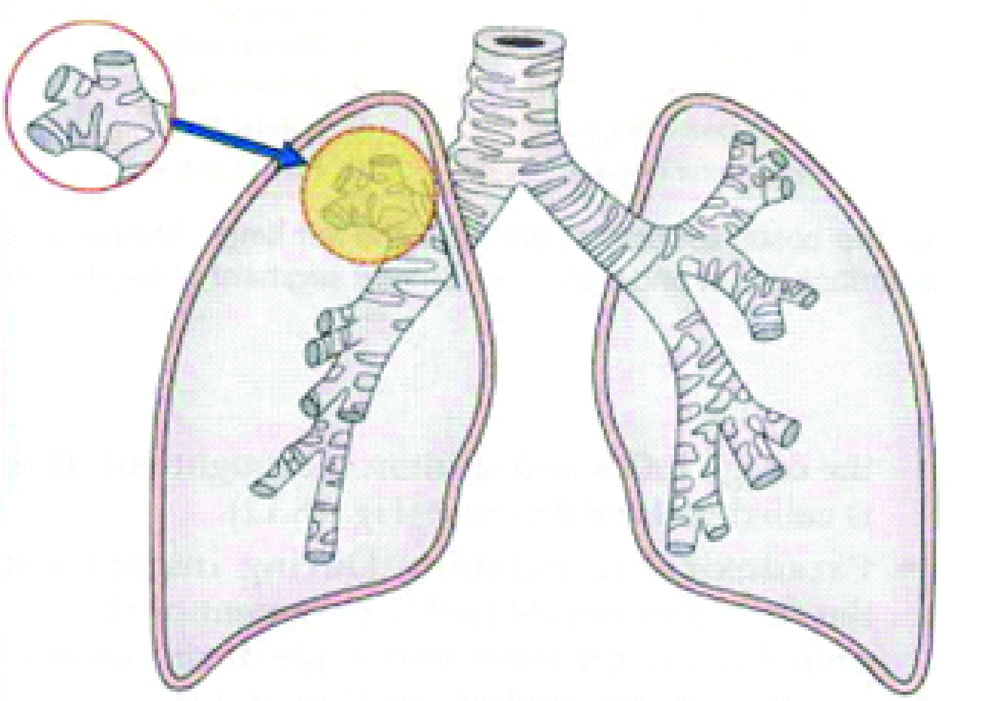
The golden ratio can also be found in the lungs. The presence of asymmetrical branching lung structure proved the existence of golden ratio. The irregular branching configuration of the bronchial tree in mammals is in accordance with a process by Fibonacci [Table/Fig-12]. Goldberger AL et al., confirmed the fact of the Golden Ratio. Each bronchus branches into two unequally sized bronchioles, with the ratio of these two tubes approximating the Golden Ratio. This pattern continues throughout the bronchial tree demonstrating a relative proportion roughly equal to phi. This confirms that breathing is not a one step process, rather it is a system of discrete steps. This knowledge has been applied in the development of biological variable ventilators. The variable ventilation followed a fractal pattern that corresponded with the natural branching found within the patients’ lungs, that is the Golden Ratio [17].
Golden ratio in bronchial tree.
Image Courtesy: BD Chaurasia’s Human Anatomy Regional and Applied Dissection and Clinical: Vol. 1: Upper Limb and Thorax
Limb Proportions
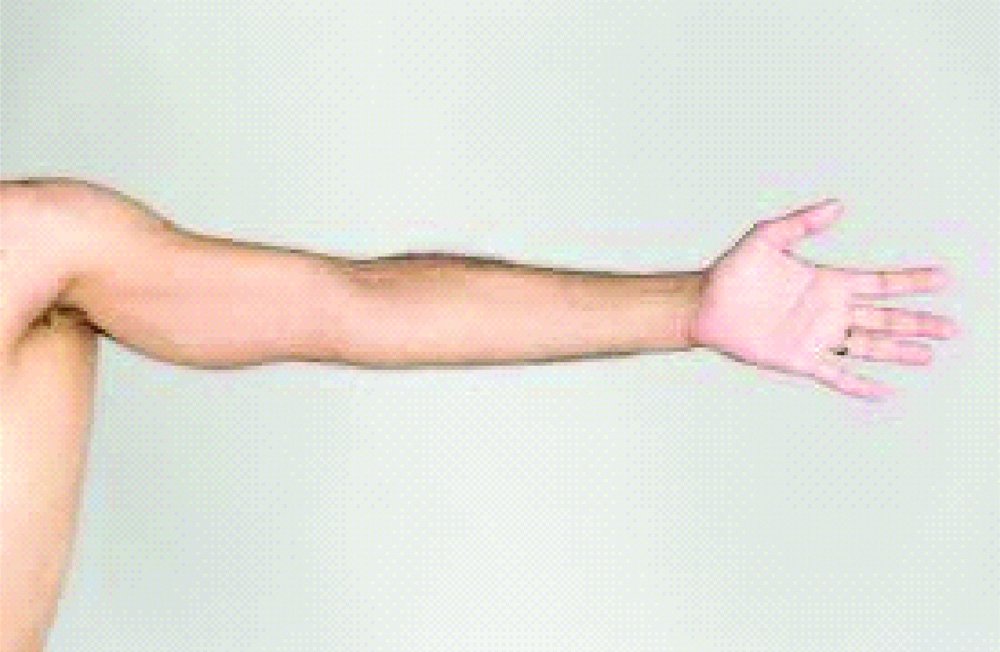
It has been observed that the golden ratio can be appreciated in the limb proportions also. Wang et al., conducted a study on the existence of golden ratio in Human upper limb. The study was conducted on 30 healthy individuals and the functional segmentsthat were included were the hand (measured from the tip of the middle finger to the wrist), the forearm (from the wrist to the elbow), and the upper arm (from the elbow to the shoulder). Based on the results of the study the authors proposed the presence of a Golden Spiral, dividing the arm into these three functional segments [Table/Fig-13a,b] [18].
Proportion in human hand.
Galaxies
The orbital relation between the planets also follows golden proportional. The distance from Mercury to Venus is approximately 1.618 times the distance from the Sun to Mercury and the distance from Earth to Mars is approximately 1.618 times the distance from Venus to Earth. There is an evolving theory which suggests that the universe may actually be in the shape of a dodecahedron based on the Golden Proportion [Table/Fig-14].
Golden proportion in elliptical galaxies.
# Public domain

Johannes Kepler, (1571-1630) the discoverer of the elliptical nature of the orbits of the planets around the sun, described the Golden Proportion as: “Geometry has two great treasures: one is the other, the division of a line into extreme and mean ratio. The first wemay compare to a measure of gold; the second we may namea precious jewel’’ [8].
ART and Architecture
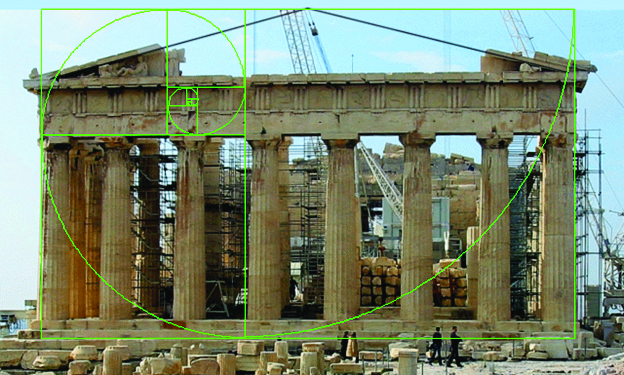
The golden proportion was also known to the ancient Greeks. This awareness prejudiced their art and architecture. The primary application of this proportion perhaps can be observed in the Egyptian pyramids, where it was used for designing the great pyramids of Giza. The majority of the ancient Greek buildings, including the Parthenon, considered being antiquity’s most perfect structure was built on the ideologies of Golden proportion. Phidias who was credited with the discovery of phi sculptured many architectural masterpieces including Parthenon. Parthenon was built in 440BC at the Temple of Athena on the Acropolis in Athens. The Parthenon’s facades as well as elements of its facade were built in the golden rectangles. The altitude was constructed in the proportion 1.0 and the base was 1.618 times the altitude. The golden rectangles were also formed in the spaces between the columns [Table/Fig-15a].
Golden ratios in famous architectures; The Parthenon.
Image Courtesy: Meisner G. The Parthenon and Phi, the Golden Ratio. 2013.
The famous cathedral Notre de Dame in Paris shows the integration of the golden proportion. The concept also find its representation in world renowned monument “Taj Mahal” constructed in 1648 by the Mughal Emperor Shahjahan, in Agra, [Table/Fig-15b] India and also in modern architecture marvels like United Nations building in New York, The CN Tower in Toronto and “Golden Ratio” sculpture in Jerusalem [8].
Golden ratios in famous architectures; The Taj Mahal.
Image Courtesy: Meisner G. Phi and the Golden Section in Architecture. 2013.

Leonardo da Vinci (1451- 1519) included golden proportion in his famous paintings namely the “Vitruvian Man”, “The Last Supper” and the “Mona Lisa”.
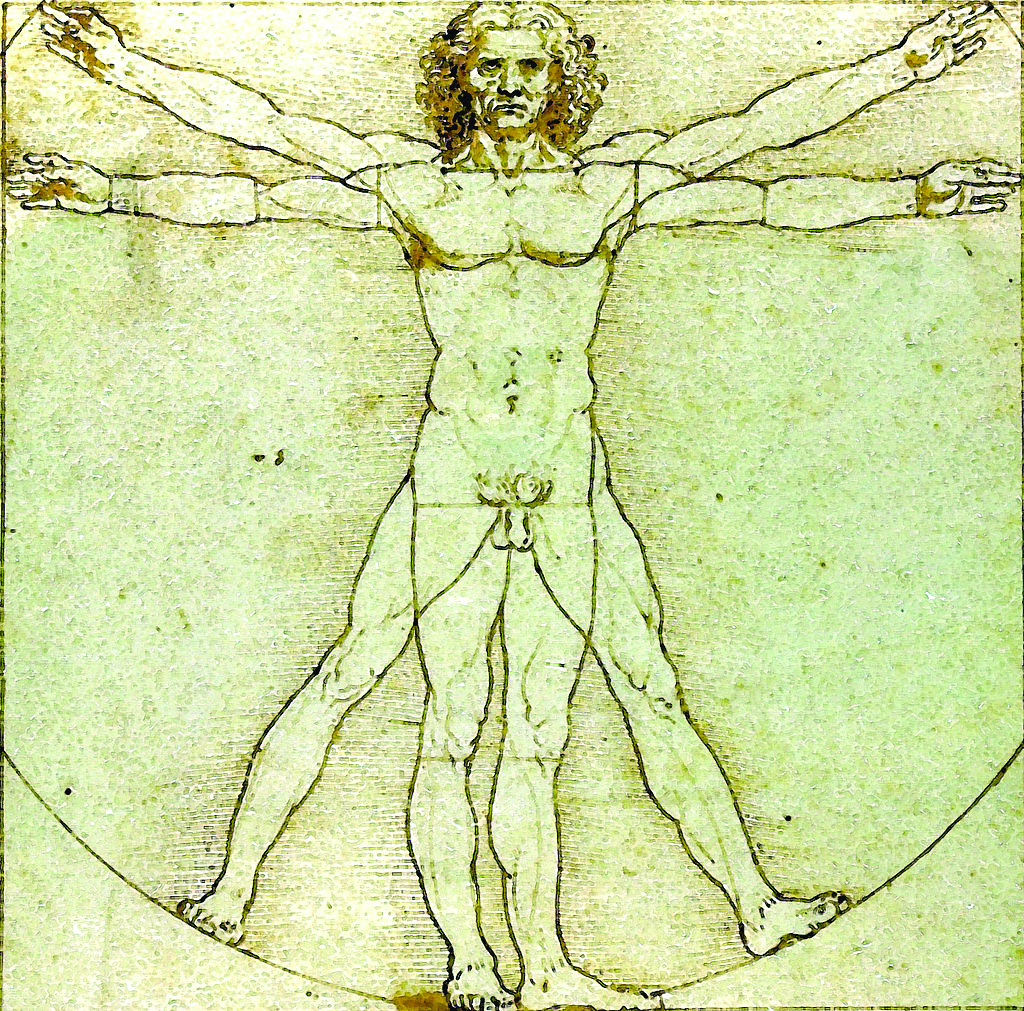
The vitruvian man image illustrates a nude man inscribed in a circle with arms and legs outstretched like spokes in a wheel. The distance from the top of the man’s head to the middle of his chest is 1.618 times the length of the head alone and the distance from the top of his head to his navel is 1.618 times the distance from his head to the middle of the chest, and so on [Table/Fig-16] [8].
Golden ratios in famous art: “The Vitruvian man”.
# Public domain
The famous paintings of Mona Lisa” is also said to have the golden ratios in its geometric equivalents [8]. The assessment of the painting discloses many golden rectangles. Golden rectangle can be appreciated around her face. The line that divides the rectangle crosses the eyes resulting in another golden rectangle. This also makes the proportion of her head length to her eyes as golden. The rectangle formed from right wrist to her left elbow extending vertically till the head also forms the golden rectangle [Table/Fig-17]. If we draw squares inside this Golden Rectangle, we will ascertain that the boundaries of these new squares emanate to all the important focal points of her face: chin, eye, nose, and the mouth [8].
Unravelling golden ratio in Mona Lisa.

Aesthetics
Facial Beauty
Beauty lies in the eyes of the beholder is commonly said, however it is believed that the world is beautiful because there is a certain order, harmony, measure and proportion between its elements. Golden Proportion has been considered as the ideal ratio for defining beauty. The universal standard for the facial beauty is also based upon the golden proportion regardless of the race, age, and gender. The universal standard is based on the divine proportion [8]. Ricketts proved that the harmonious faces of beautiful women followed golden proportions [19]. Many studies have concluded that beautiful faces have facial measurements close to the golden ratio [20-25]. Jefferson Y also stated that beautiful faces have idyllic facial proportion and the ideal proportion is directly related to divine proportion [26]. Pallett PM in 2010, did four experiments to test the presence of an ideal facial feature arrangement that could optimise the attractiveness of any face. Between identical facial features where the eye-mouth distances and interocular distances were different, paired comparison of attractiveness was made. The result of the study revealed that the facial attractiveness is maximised when the horizontal distance between the eyes is approximately 46% of the face’s width and the vertical distance between the eyes and the mouth is approximately 36% of its length of face [27].
Kiekens RM et al., analysed the relationship between facial esthetics and golden proportions in adolescents. They concluded that beautiful faces showed less deviation from the golden standard [24].
Panchers H et al., in 2010, compared attractive and non attractive faces of females and males with respect to the presence of the divine proportions. They also found that attractive individuals have facial proportions approximating to the divine proportion values in comparison to those who were non attractive [21]. This is in accordance with the hypothesis of Ricketts that facial beauty can be measured to some degree.
The study done by Packiriswamy V et al., in 2012, aimed to study the facial morphology and identify individuals with normal, short, and long face in 300 Malaysian nationality subjects. The parameters measured were facial height and bizygomatic width of face, and physiognomical facial index was calculated. The faces were classified on the basis of Golden proportion rule. When the ratio approximated to 1.6, the shape was considered to be normal; when its ratio was larger than 1.6, the shape was long; and when the ratio was smaller than 1.6, the shape was considered to be short. Independent t test was used to test the difference between sexes and among the races. They found significant variation in the facial morphology according to gender and race in the population. In Malaysian Chinese subjects, maximum number of subjects (n=77) had a short face, In Malaysian Indian subjects, maximum number of subjects (n=75) had a short face, and in Malay subjects, 72 subjects had a short face. A total of 16 Malaysian Chinese subjects, 20 Malaysian Indian subjects, and 24 Malay subjects had a normal size face [28]. Majority of subjects had faces which did not follow the golden proportion.
A recent study done by Alam MK in 2015 showed contradictory results. They concluded that there is no significant association between golden ratio and facial evaluation score among Malaysian population. According to their study individuals who find themselves attractive may not have facial measurements which approach the golden ratio [29].
As the literature shows varied results, it cannot be conferred that Divine proportions can be considered in Malaysian populations for defining beauty.
In a study by Saraswathi P only 14 subjects out of 75 had a normal face shape, according to the golden proportion rule [30].
Marquardt developed a beauty mask based on the divine proportion and showed that, a face is deemed beautiful if it conforms to this beauty mask regardless of race or age [31]. He also discovered golden rectangle, according to which the height of the central incisor is within the golden proportion to the width of the two central incisors.
Rupesh S et al., concluded that the measured proportions in facial profiles with the higher esthetic scores were closer to the divine proportion than with the lowereesthetic scores [32].
Association of Facial Proportions and Human Health
According to the studies done in the past the ideal facial proportions are based on the golden proportion. A deviation from this proportion can result in health problems. For example, the patients with long face syndrome may have a greater tendency towards of mouth breathing, as such patients have difficulty in breathing through nose due to narrow sinus cavity that inhibits air flow; and the patients with short face syndrome may have abnormal jaw development and an incidence of craniofacial pain and headaches due to migraine [7,8].
Golden Proportion and Dental Health
Facial beauty correspondes with anatomical symmetry and with mouth and teeth. Thus, professionals in the field of dentistry have tried to characterise the parameters of an aesthetically appealing smile.
Mack MR highlighted the importance of treating the dentition according to the face based on the divine proportion. He stated that the lowed one-thirds of the face significantly impacts the facial appearance. He also warned that the complications may appear in facial esthetics when only mounted casts were used for diagnosis [33].
In 1973, Lombardi officially proposed the existence of having proportionate teeth, but rejected the idea of using golden proportion to create aesthetic teeth [34].
Levin in 1978, was the first to observe that the width of maxillary central incisor is in golden proportion to the width of the lateral incisor and width of lateral incisor is in golden proportion to the width of canine. He later developed a tooth caliper based on this observation. This proportion has been combined in a grid, called the diagnostic grid or the golden proportion grid which can be used to assist in perfecting the esthetics of the anterior teeth [Table/Fig-18]. These grids are available in seven sises to accommodate all widths of the central incisor from 7 mm to 10 mm in steps of 1/2 mm [35].
Illustration of golden ratio in anterior teeth.
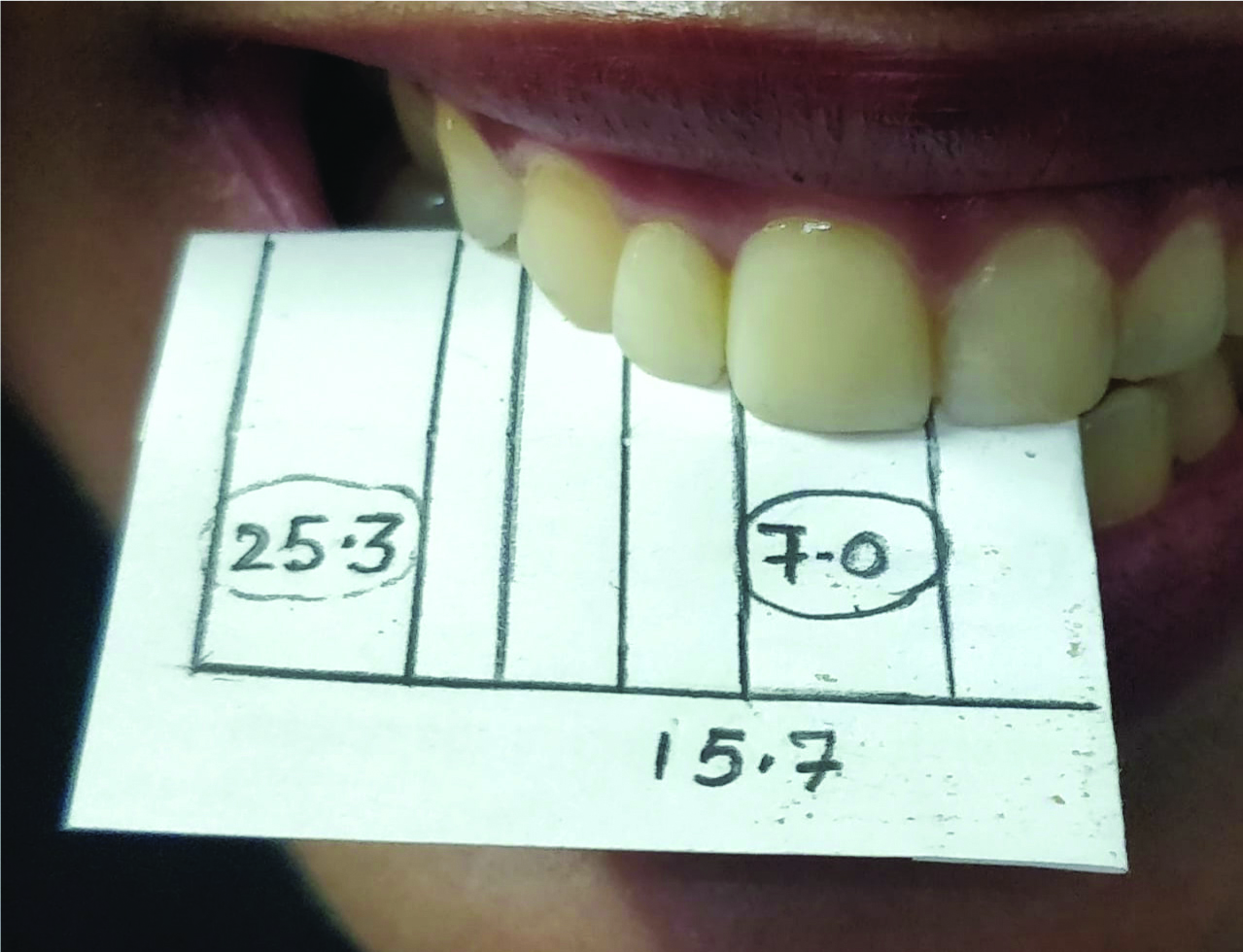
Relationship also exits between the pleasant smile and the neutral space. The neutral space is defined is a dynamic space which appears in a broad smile and can be defined as a bilateral space bounded laterally by the corner of the smiling mouth and medially by the dental arch.
Further research into the relationship between golden proportion, dental arrangement and aesthetic smile was developed by Rickets in 1982. He implemented the use of golden proportions in the treatment of patients such as guides for planning orthognathic surgeries. He suggested the use of 13 skeletal ratios in lateral and frontal radiographs which should ideally follow the divine proportion in order to obtain a beautiful face [36].
In a study by Bragatto FP et al., it was concluded that orthognathic surgery had little influence on the studied proportion and that the golden ratio was not present in majority of the ratio as given by ricketts; neither before nor after the surgery [37].
In a study by Subhashini MHR et al, it was observed that the ratio of 1.2 was more commonly perceived in 89% of individuals than 1.618 and 1.3 in only 11% of samples of south Indian population. This is because the central incisor in this population is slightly smaller and canine is slightly larger than the ideal golden proportions. Despite this, the ideal golden ration can be applied clinically [38].
Conclusion
The nature’s numbering system appears everywhere. Though there are other numbering systems also, the present review highlights the application of Fibonacci numbers in nature, human body and architecture which is considered as the key to esthetics. With regards to the anecdotal evidence of applications of the Fibonacci numbers in the field of medical literature, further studies are recommended. This will help in substantiating the esthetic correction and treatment planning; and authenticate its application from different perspectives.
[1]. Leonardo Pisano Fibonacci. Available from- http://www-history.mcs.st-andrews.ac.uk/Biographies/Fibonacci.html. Last accessed on 18th October 2019 [Google Scholar]
[2]. Mastin L, The story of Mathematics 2010 Available from- https://www.storyofmathematics.com/medieval_fibonacci.html. Last accessed on [Google Scholar]
[3]. Bortner C, Peterson A. The history and applications of fibonacci numbers. University of Nebraska-Lincoln, UCARE, Spring 2016 Research Fair Poster. 2016 [Google Scholar]
[4]. Fibonacci Smile. Available from: https://www.fibonaccismile.com/what-is-fibonacci. Last accessed on 18th October 2019 [Google Scholar]
[5]. Knott R. The Lucas Numbers. 2017. Available from: http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/lucasNbs.html. Last accessed on 18th October 2019 [Google Scholar]
[6]. Ghose T. What Is the Fibonacci Sequence? 2018. Available from: http://www.livescience.com/37470-fibonacci-sequence.html. Last accessed on 18th October 2019 [Google Scholar]
[7]. Rofman S. To what extent is there a biological basis for the Golden Ratio? Available from: https://3gjb993i3yk5b587o4gvsbos-wpengine.netdna-ssl.com/ wp-content/ uploads/2018/09/sam_rofman_epq.pdf. [last accessed on 18th October 2019] [Google Scholar]
[8]. Saraf S, Saraf P, The Golden Proportion: Key To The Secret Of BeautyThe Internet Journal of Plastic Surgery 2013 9(1):01-16.10.5580/2ce6 [Google Scholar] [CrossRef]
[9]. Sudipta Sinha, The Fibonacci Numbers and Its Amazing ApplicationsInternational Journal of Engineering Science Invention 2017 6(9):07-14. [Google Scholar]
[10]. Lin Y, Peng W, Chen H, Liu Y, Fibonacci numbers in daily lifeAvailable from: https://studyres.com/doc/159921/fibonacci-numbers-in-daily-life. Last accessed on 18th October 2019 [Google Scholar]
[11]. Schroeder K, The social dynamics of beesScience 2018 Available from: http://nouse.co.uk/2018/03/06/the-social-dynamics-of-bees. Last accessed on 18th October 2019 [Google Scholar]
[12]. Hamilton R, Dunsmuir RA, Radiographic assessment of the relative lengths of the bones of the fingers of the human handJ Hand Surg Br 2002 27:546-48.10.1054/jhsb.2002.082212475513 [Google Scholar] [CrossRef] [PubMed]
[13]. Henein MY, Zhao Y, Nicoll R, Sun L, Khir AW, Franklin K, The human heart: Application of the golden ratio and angleInternational Journal of Cardiology 2011 150(3):239-42.10.1016/j.ijcard.2011.05.09421703707 [Google Scholar] [CrossRef] [PubMed]
[14]. Yalta K, Ozturk S, Yetkin E, Golden Ratio and the heart: A review of divine aestheticsInternational Journal of Cardiology 2016 24:107-112.10.1016/j.ijcard.2016.03.16627060268 [Google Scholar] [CrossRef] [PubMed]
[15]. Prasanth G, Narasimha-ShenoiGOLDEN RATIO IN HUMAN ANATOMY. THESIS PDFDOI: 10.13140/2.1.2265.9526 [Google Scholar]
[16]. Pietsch M, Davilla LA, Erfurt P, Avci E, Lenarz T, Kral A, Spiral Form of the Human Cochlea Results from Spatial ConstraintsSci Rep 2017 7:750010.1038/s41598-017-07795-428790422 [Google Scholar] [CrossRef] [PubMed]
[17]. Goldberger AL, West BJ, Dresselhaus T, Bhargava V, Bronchial asymmetry and Fibonacci scalingExperientia 1985 41(12):1537-38.10.1007/BF019647944076397 [Google Scholar] [CrossRef] [PubMed]
[18]. Wang N, Ma J, Jin D, Yu B, A Special Golden Curve in Human Upper Limbs’ Length Proportion: A Functional Partition Which Is Different from AnatomyBioMed Research International 2017 2017:01-06.10.1155/2017/415856128232941 [Google Scholar] [CrossRef] [PubMed]
[19]. Ricketts RM, The golden dividerJ Clin Orthod 1981 15(11):752-59.pmid:6948819 [Google Scholar]
[20]. Medici Filho E, Martins MV, dos Santos da Silva MA, Castilho JC, de Moraes LC, Gil CT, Divine proportions and facial esthetics after manipulation of frontal photographsWorld J Orthod 2007 8:103-08.pmid:17580503 [Google Scholar]
[21]. Panchers H, Knapp V, Erbe C, Heiss AM, Divine Proportions in Attractive and nonattractive facesWorld J Orthod 2010 11(1):27-36.pmid:20209174 [Google Scholar]
[22]. Moss JP, Linney AD, Lowey MN, The use of three-dimensional techniques in facial estheticsSemin Orthod 1995 1(2):94-104.10.1016/S1073-8746(95)80096-48935048 [Google Scholar] [CrossRef] [PubMed]
[23]. Tripathi AA, Tandon RP, Hantodkar N, Facial Divine Proportions in Attractive North Indian Females: A Photographic StudyWorld J Dent 2014 4(1):41-46.10.5005/jp-journals-10015-1200 [Google Scholar] [CrossRef]
[24]. Kiekens RM, Kuijpers-Jagtman AM, van ’t Hof MA, van ’t Hof BE, Maltha JC, Putative golden proportions as predictors of facial esthetics in adolescentsAm J Orthod Dentofacial Orthop 2008 134(4):480-83.10.1016/j.ajodo.2006.10.04118929264 [Google Scholar] [CrossRef] [PubMed]
[25]. Schmid K, Marx D, Samal A, Computation of a face attractiveness index based on neoclassical canons, symmetry, and golden ratios 2006Faculty Publications, Department of Statistics, University of NebraskaPaper 12 [Google Scholar]
[26]. Jefferson Y, Facial beauty-establishing a universal standardInt J Orthod Milwaukee 2004 Spring 15(1):09-22. [Google Scholar]
[27]. Pallett PM, Link S, Lee K, New “golden” ratios for facial beautyVision Res 2010 50(2):149-54.10.1016/j.visres.2009.11.00319896961 [Google Scholar] [CrossRef] [PubMed]
[28]. Packiriswamy V, Kumar P, Rao M, Identification of facial shape by applying golden ratio to the facial measurements: An interracial study in Malaysian populationNorth Am J Med Sci 2012 4:624-29.10.4103/1947-2714.10431223272303 [Google Scholar] [CrossRef] [PubMed]
[29]. Alam MK, Mohd Noor NF, Basri R, Yew TF, Wen TH, Multiracial Facial Golden Ratio and Evaluation of Facial AppearancePLOS ONE 2015 10(11):e014291410.1371/journal.pone.014291426562655 [Google Scholar] [CrossRef] [PubMed]
[30]. Saraswathi P, The golden proportion and its application to the human faceEur J Anat 2007 11(3):177-80. [Google Scholar]
[31]. Marquardt SR, The Golden decagon and human facial beautyJ Clin Orthod 2002 36:339-47. [Google Scholar]
[32]. Rupesh S, Rakesh S, Winnier J J, Kaimal A, John A, Prasannan M, The role of divine proportion in the perception of beauty: a cross sectional studyAmrita Journal of medicine 2014 10(1):01-44. [Google Scholar]
[33]. Mack MR, Vertical dimension: a dynamic concept based on facial form and oropharyngeal functionJ Prosthet Dent 1991 66:478-85.10.1016/0022-3913(91)90508-T [Google Scholar] [CrossRef]
[34]. Lombardi RE, The principles of visual perception and their clinical application to denture estheticsJ Prosthet Dent 1973 29:358-82.10.1016/S0022-3913(73)80013-7 [Google Scholar] [CrossRef]
[35]. Levin E, Dental esthetics and the golden proportionJ Prosthet Dent 1978 40:244-52.10.1016/0022-3913(78)90028-8 [Google Scholar] [CrossRef]
[36]. Ricketts Rm, Divine proportion in facial estheticsClin Past Surg 1982 [Google Scholar]
[37]. Bragatto FP, Chicarelli M, Kasuya AV, Takeshita WM, Iwaki-Filho L, Iwaki LC, Golden Proportion Analysis of dental-Skeletal patterns of classII and III patients pre and post orthodontic- orthognathic treatmentJ Contemp Dent Pract 2016 17(9):728-33.10.5005/jp-journals-10024-192027733715 [Google Scholar] [CrossRef] [PubMed]
[38]. Subhashini MHR, Prasad MKV, Jain AR, Incidence of goldon proportion among the target south indian populationJournal of Pharmacy Research 2018 12(1):20-23. [Google Scholar]