In the scientific literature, it is well known that stature is significant parameter to evaluate some situations in humans [1]. For instance, stature measurement is necessary for the estimation and standardisation of physiological parameters such as evaluation of growth and development of children, assessment of nutritional indices, lung capability, muscle strength, glomerular filtration rate, resting metabolic rate, and regulation of drugs quantity [2]. In some cases, such as deformities of the limbs, fractures, paralysis, scoliosis, lower limb amputations, contractures, or especially in elderly people who are unable to stand due to mobility problems and kyphosis, the stature of the individual can not be determined precisely by direct measurements [2-6]. Detection of real stature may be difficult in physically and mentally weak hospitalised patients who are wheelchair-bound or bedridden and have osteoporosis, deformation after hip fractures or paralysis [5]. In addition, it is essential as it supplies a forensic anthropological estimate of the stature of a person in the living state; playing a significant role in the identification of individuals [1].
Recent studies have reported the validity of using various parameters in estimating statures, such as upper and lower extremities [7-10], sternum [11], vertebral column [12], hand and footprints [13], cephalo-facial dimensions [14] and arm span [1,15-20]. Among all these parameters used as an alternative to estimate stature, arm span was found to be a very important parameter for age-related loss in stature as per the previous studies.
The analysis of dimensional relationships between body parts and the entire body has been the centre of interest many years for scientists, anatomists and anthropologists. Several regression equations have been developed for this purpose [2]. When entire body parameters are examined, correlation between stature and the arm span was found to be the most reliable. This strong interrelationship between stature and arm span varies considerably among different ethnic and racial groups [1,4,5,15,20-23]. For instance, Hickson and Frost applying the Bland & Altman agreement analysis reported a very weak agreement between the stature and arm span although these correlate quite well. They have recommended that arm span measurements may not be suitable parameter for stature estimation in some populations [6]. Even though several studies have been done in this regard, the database for the Turkish population is insufficient [21,24].
In this context; the objective of the present study was to investigate the interrelationship between arm span and stature measurements in a sample of Turkish adults and then develop the reference regression equations for estimating stature for both sexes.
Materials and Methods
Subject Enrollment
The sample group used for this cross-sectional study consisted of high school students from the Karadeniz Technical University (KTU), Trabzon, Turkey. KTU, Vocational School of Health Science, consists of four programs including health education. It accepts students from all geographic regions of Turkey regardless of ethnic origin and socio-economic status. The study period was from February 2016 to April 2018 and it was based on the principle of volunteerism.
The sample size was predicted using 80% power at the 5% level of significance in accordance with standard statistical protocol [25]. The total number of students who were enrolled in the courses during the 2016-2017 academic year of the university was 613. Approximately 70% of this number is made up of female students (187 males, 426 females). Because of the fact that the students who enrolled in the study were of mostly females, stratified randomisation method was used according to sex. An internal cross-validation approach in which the total sample was split randomly into two groups. A total of 274 individuals (137 male, 137 female) were included as the research group, and 50 individuals (25 male, 25 female) were included as the control group. The reliability of the equations was evaluated by blind method in the control group.
For both research and control group, the eligibility criteria for recruitment of the individuals included age range between 20-27 years, apparently healthy individuals with no physical deformity. All participants were born and grew up in Turkey and have a Turk ethnic background. This particular age group was preferred because the growth of an individual ceases by this age and that there was no age-related decrease in stature at this age [4]. Exclusion criteria for research and control groups were as follows: presence of physical deformities that could affect stature or arm span, difficulty in extending arms and non-Turkish ethnicity. All subjects signed an informed consent form. Ethical approval was obtained from the University Ethics Committee (protocol no: 24237859-508; approval no: 2016/87).
Evaluation
Stature and arm span were measured for all the participants according to the standard anthropometric protocols of the International Society for the Advancement of Kinanthropometry (ISAK) [26]. All measurements were recorded in centimetres (cm) to the nearest millimetres (mm). The stature was measured from the highest point on the head to the floor obeying the anatomical position and Frankfurt plane by portable stadiometer (SECA 213). It was measured to the nearest 1 mm in bare feet with the subjects standing upright against a stadiometer. The arm span length was obtained by measuring the distance from the right middle fingertip to the left middle fingertip. The participants were asked to be in a standing position with back to the wall and outstretch both arms, 90° abduction with palms facing forwards. Arm span measurement included the shoulder width [Table/Fig-1], and was measured with tape-measure in centimetre with the precision of 0.5 cm.
Procedure of stature and arm span measurements.
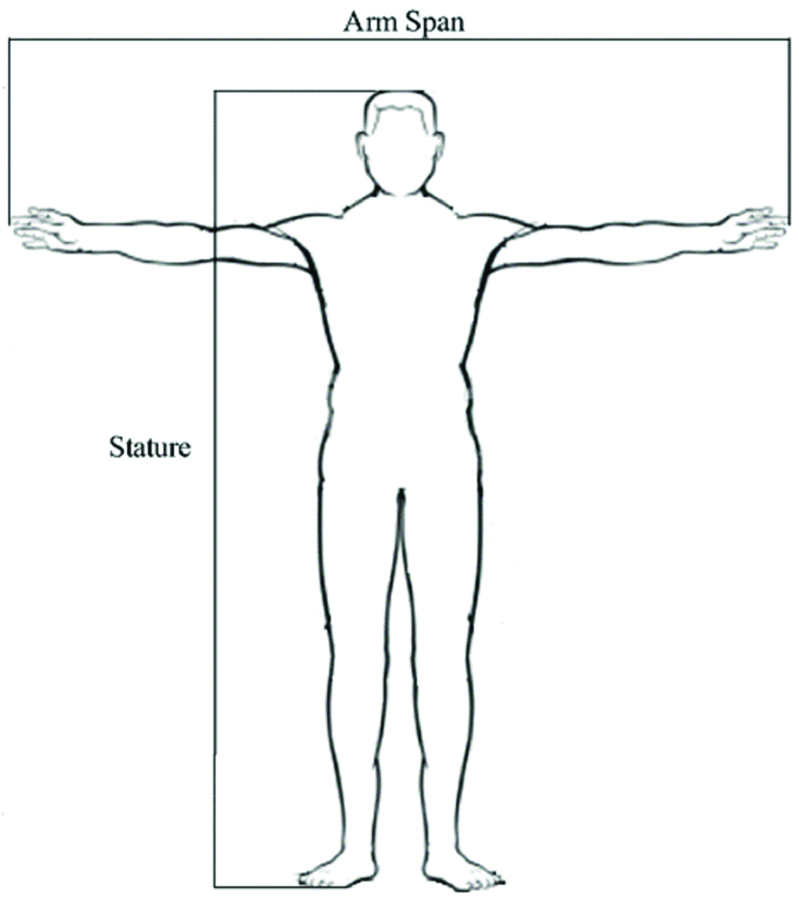
It is known that there may be a difference in the stature of the individuals about 1.5 cm between the time of awakening in the morning and the last hours of the day. In the first hours of day, the stature is at the highest level and descends to the lowest level in the evening hours [27]. For this reason, measurements were performed at the same time of day between 1 and 3 PM to avoid diurnal variation. To prevent interpersonal error all measurements were taken by the same person. Each participant was measured twice, and an average of the two readings was recorded. When the two records for each variable fell within 4 mm of each other, their average was taken as the best estimate for the exact value. If two measurements did not provide 4 mm standardisation, two additional measurements were taken and the average of the nearest records was used as the best score [7].
While conducting the current study, the absolute Technical Error of Measurement (TEM) was taken into consideration. TEM is a valid analysis for anthropometrical measurements and indicates the measurement accuracy. Before collecting data, arm span and stature measurements were taken from 40 subjects (20 males, 20 females, using stratified randomisation method according to sex). The sample was taken from the research group of 274 subjects. Measurements were made twice and on two separate days. TEM was calculated using the following equation: In this formula, D indicates the difference between two measurements and N is the number of individuals.
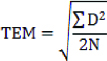
The relative Technical Error of Measurement (rTEM) was calculated from two consecutive set of measurements by dividing the TEM for a given variable by the grand mean of that variable and multiplying the result by 100. The coefficient of Reliability (R) and Coefficient of Variation (CV) was calculated by following equation.
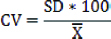
In this equation, X̄ is the average of measurements and SD is the standard deviation. The CV shows sample variability relative to the mean of the sample [28]. TEM and reliability were found to be within the acceptable standards for arm span and stature measurements (R>0.9; rTEM<5%), as shown [Table/Fig-2,3].
The results of TEM analysis in research group.
| a | b | d2 | TEM | rTEM (%) | R |
|---|
| Stature | 1687.25±99.05 | 1719.36±98.37 | -32.11±3.88 | 22.87 | 1.34 | 0.95 |
| Arm span | 1675.5±109.92 | 1701.37±110.27 | -25.87±5.58 | 18.70 | 1.11 | 0.97 |
n=40; a: average of the first measurement; b: average of the second measurement; d2: difference between the average; TEM: measure technical error; rTEM: relative technical error of measurement; R: coefficient of reliability
Average, standard deviation and coefficient of variation of stature and arm span in research group.
| X̅ | SD | CV |
|---|
| Stature | 1703.30 | 98.71 | 5.80 |
| Arm span | 1688.43 | 110.10 | 6.52 |
n=40; CV: Coefficient of variation; SD: Standard deviation; X: Average
Statistical Analysis
Statistical analysis was performed on SPSS (Version 23.0, SPSS Inc., Chicago, IL, USA). A p-value of <0.05 was considered statistically significant. Descriptive analysis was performed, and numeric data were presented as mean±standard deviation. An unpaired t-test was used to compare arm span and stature measurements between males and females in research group. The inter-relationships between stature and arm span were determined by Pearson correlation coefficient with 95% confidence interval. In the research group, models were developed using linear regression analysis for stature estimation. Regression coefficient and constants were calculated to estimate the stature from regression equation (Y=a+bX). Stature=value of constant+regression coefficient x arm span. The Standard Error of Estimate (SEE) shows the deviation of predicted stature from the real stature. A low value of SEE indicates greater reliability in the predicted stature. Scatter diagrams and regression lines were plotted from the data.
The most important element in determining the simple regression model adequacy is the examination of residuals. For this purpose, studentised residual analysis was carried out in this study. It can be expressed that if the residuals are in the range of (-2 +2) with 0 mean and ±1 standard deviation, and the residuals are normal distribution, the model is sufficient. Kolmogorov-Smirnov test was used to evaluate the normality distribution of data for studentised residual analysis. The power of the equations was also evaluated by G-power analysis [29].
The similarity of the estimated stature measurements to the real stature measurements was assessed by the unpaired t-test and the Intraclass Correlation Coefficient (ICC). In order to check validation and the reliability, the stature measurements of the control group were estimated using the developed regression models.
Results
Participant General Characteristics
A total of 324 volunteers were enrolled in investigation, including 137 male and 137 female for research group and 25 male and 25 female for control group. The mean and standard deviations of the stature and arm span values and the differences between two parameters in both sexes for research and control groups are presented in [Table/Fig-4]. As shown, males were found to be taller in stature and arm span measurements compared to the females (p<0.05).
Descriptive statistics for males and females in research and control groups.
| Measures | RG male (n=137) Mean±SD | RG female (n=137) Mean±SD | CG male (n=25) Mean±SD | CG female (n=25) Mean±SD | p-value |
|---|
| Stature | 1735.62±66.95 | 1602.18±61.53 | 1742.40±65.01 | 1612.00±60.96 | <0.001 |
| Arm span | 1741.53±66.60 | 1589.48±67.46 | 1748.00±70.94 | 1612.40±71.72 | <0.001 |
Unpaired t-test; CG: Control group; RG: Research group; SD: Standard deviation
Correlations and Linear Regression Equations for Arm Span and Stature
Pearson’s correlation coefficients for stature and arm span measurements are shown in [Table/Fig-5]. Arm span has positive and significant correlations with stature in male and female groups (r=0.785, r=0.807 respectively for research group; r=0.774, r=0.885 respectively, for control group, p<0.001). Pearson’s correlation coefficients for stature was the highest in arm span of female group.
Corrrelation between stature and arm span measurements in research and control groups.
| Subject | n | r | 95% confidence interval | p-value |
|---|
| Lower | Upper |
|---|
| RG Male | 137 | 0.785 | 0.735 | 0.835 | <0.001 |
| RG Female | 137 | 0.807 | 0.753 | 0.852 | <0.001 |
| CG Male | 25 | 0.774 | 0.656 | 0.895 | <0.001 |
| CG Female | 25 | 0.885 | 0.786 | 0.950 | <0.001 |
CG: Control group, RG: Research group; R: Correlation coefficient
The scatterplots and linear regression lines are shown in [Table/Fig-6,7]. There was a positive linear relationship between stature and arm span in male and female groups (R2>0.7; p<0.001). The scatterplots indicate that these regression equations can be used to estimate stature at the entire range of arm span with good precision. Regression equations used to estimate stature in the research group are listed in [Table/Fig-8]. Developed models for male and female groups found significant (p<0.001). The real and estimated stature for both sexes were compared using unpaired t-test and could not found significant difference (p>0.05) [Table/Fig-9].
Scatter diagram and regression line showing relationship between arm span and stature for males.

Scatter diagram and regression line showing relationship between arm span and stature for females.

Results of linear regression analysis in research group for males and females.
| Group | Regression equation | R | SEE | R2 | Adj R2 | t | p-value | Power 1-β |
|---|
| Male | S=420.527+ 0.755×AS | 0.785 | 4.163 | 0.716 | 0.713 | 14.724 | <0.001 | 1.000 |
| Female | S=432.536+ 0.736×AS | 0.807 | 3.649 | 0.751 | 0.748 | 15.869 | <0.001 | 1.000 |
Adj R2: Adjusted R-squared; AS: Arm span; R: Regression coefficient; R2: coefficient of determination; S: Stature; SEE: Standard error of estimate; t: t statistics; Power 1-β: error probability
Comparison between measured and estimated stature.
| Group | n | Measured Stature | Estimated Stature | t | p-value |
|---|
| Male | 137 | 1735.62±66.95 | 1731.15±56.99 | -0.596 | >0.05* |
| Female | 137 | 1602.18±61.53 | 1606.66±55.24 | 0.633 | >0.05* |
| CG Male | 25 | 1742.40±65.01 | 1740.26±53.56 | 0.435 | >0.05* |
| CG Female | 25 | 1612.00±60.96 | 1619.25±52.78 | -0.385 | >0.05* |
*p>0.05 statistical significance; CG: Control group; t: t statistics
ICC estimates and 95% confidence intervals were calculated by a single-rating, absolute-agreement, two-way mixed-effects model. Values less than 0.5 are express poor reliability, values between 0.5 and 0.75 express moderate reliability, values between 0.75 and 0.9 express good reliability, and values greater than 0.90 express perfect reliability. As shown in [Table/Fig-10], values (ICC male: 0.767; ICC female: 0.873) indicate good reliability in the estimated stature.
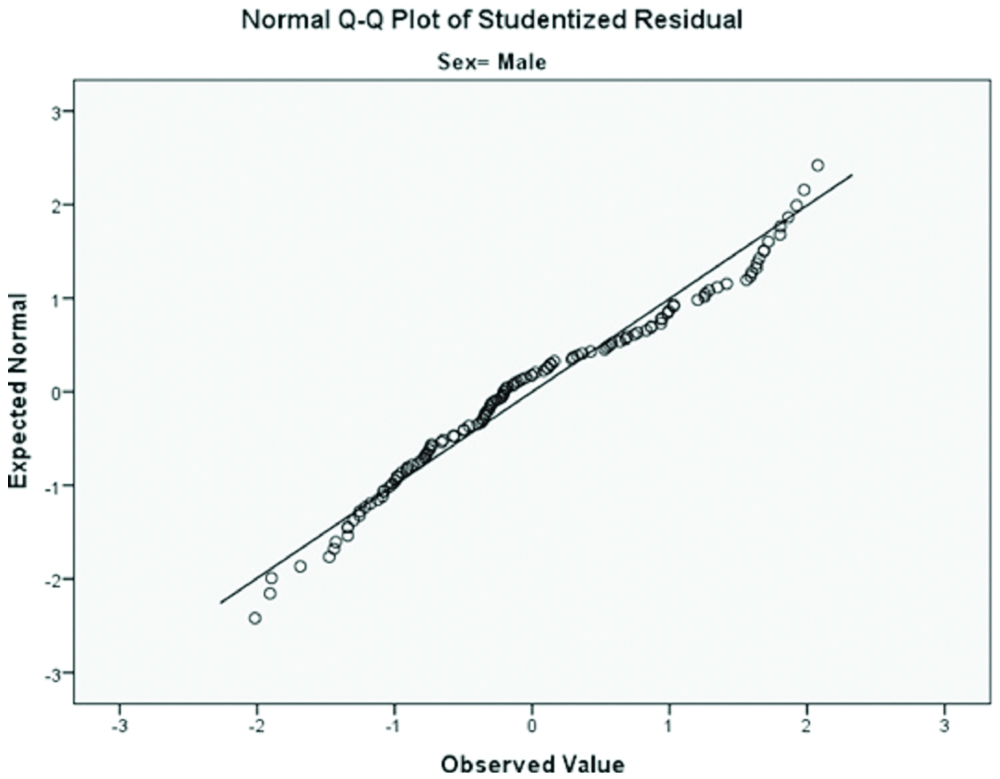
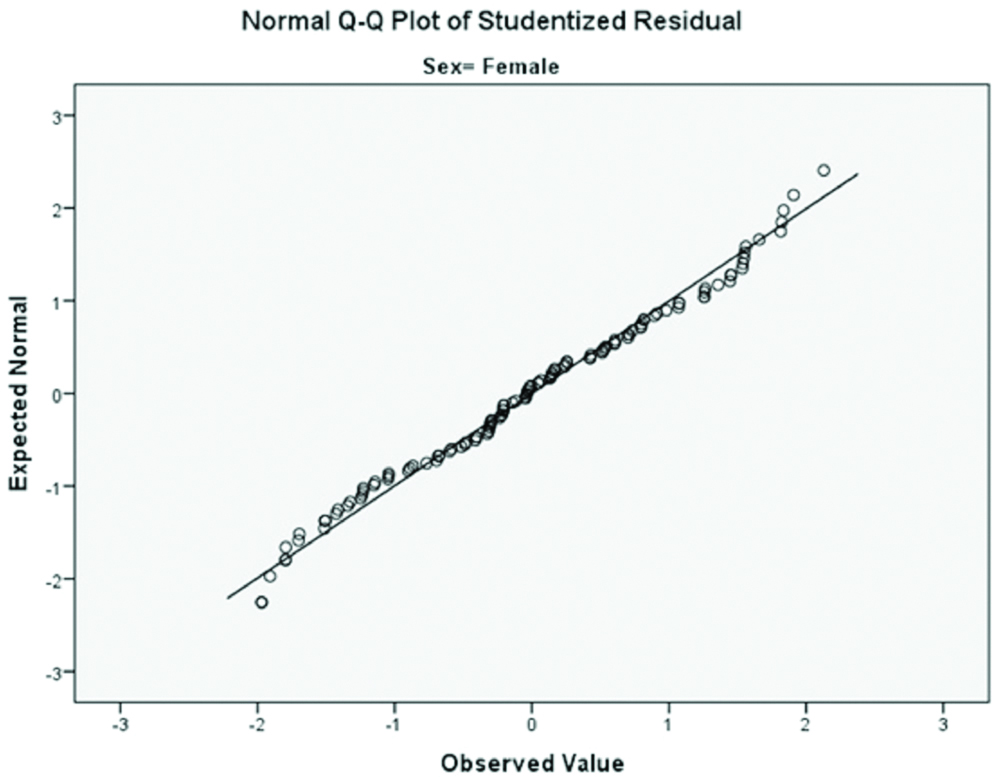
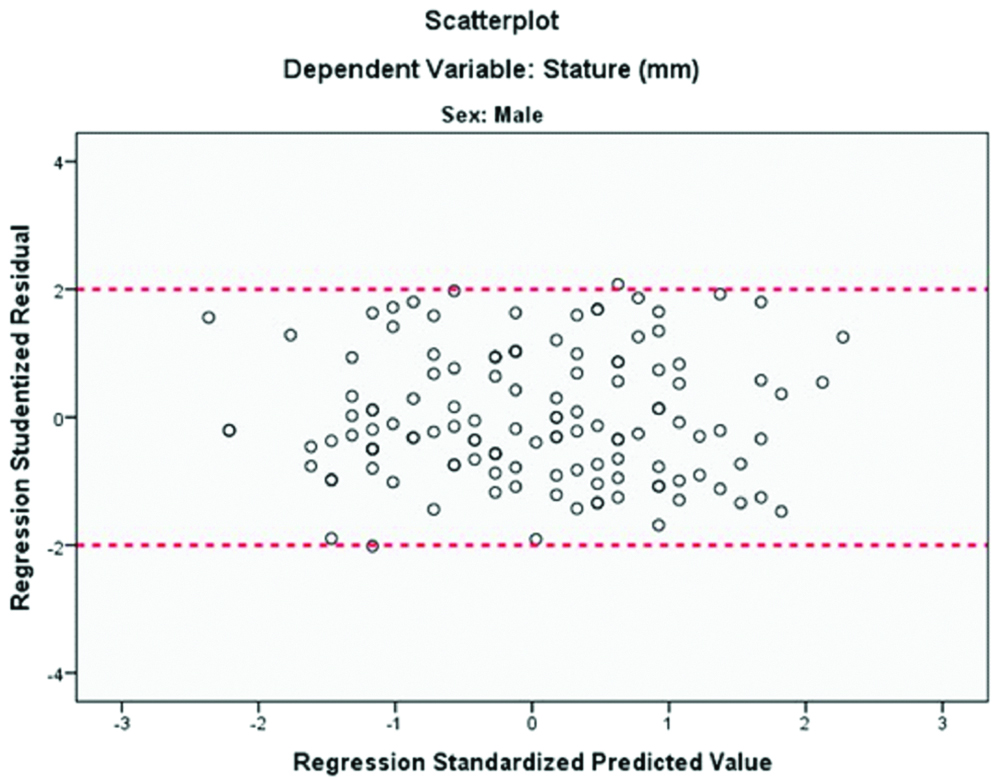
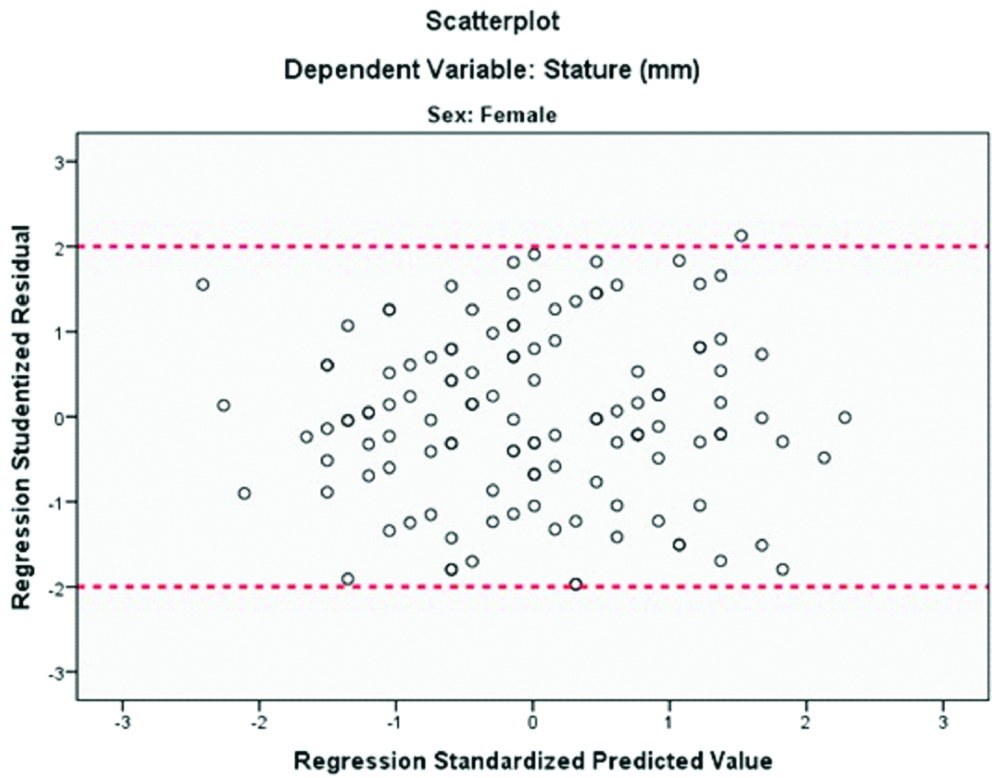
When analysing the residual analysis, it is seen that all the residues were in the range of (-2 +2) and normal distributions are observed [Table/Fig-11]. Normal Q-Q plot of studentised residual for males and females in research group was shown in [Table/Fig-12,13]. The predictive power of the equations for the G-power analysis was found quite high (p<0.001; power 1-β=1.000). Student-type residues on the y-axis were plotted against the standardised model predictions on the x-axis. Residuals scatter plots for males and females was showed in [Table/Fig-14,15].
Showing results of intraclass correlation calculation in SPSS using single-rating, absolute-agreement, 2-way random-effects model.
| | | 95% Confidence Interval | F Test With True Value 0 | |
|---|
| | ICC | Lower Bound | Upper Bound | Value | df1 | df2 | p-value |
|---|
| Single measures | Male | 0.767 | 0.537 | 0.890 | 7.333 | 24 | 24 | <0.001 |
| Female | 0.873 | 0.736 | 0.942 | 15.127 | 24 | 24 | <0.001 |
df: Degree of freedom; ICC: Intraclass correlation; Value: Value of the F Statistics
Studentised residual descriptives and normality tests in research group.
| Studentised Residual | n | Min | Max | Mean±SD | p |
|---|
| Male | 137 | -2.017 | 2.077 | 0.000±1.004 | 0.070* |
| Female | 137 | -1.970 | 2.130 | -0.000±1.004 | 0.200* |
*p>0.05 statistical significance; p: Kolmogorov-Smirnov normality test value
Normal Q-Q Plot of studentised residual for males in research group.
Normal Q-Q Plot of studentised residual for females in research group.
Residuals scatter plots for males in research group.
Residuals scatter plots for females in research group.
Discussion
Developing a linear regression equations using the arm span in estimating the stature of Turkish population sample is necessary in conditions where measurement for stature cannot be achieved due to lower extremities defects and spinal deformities, physical abnormalities that could affect stature or in situations where it is difficult or impossible to stand for example in bedridden or elderly individuals.
The results of the present study exhibited similar trends of earlier reports in terms of correlation (males: r=0.785; females: r=0.807). Mohanty SP et al., reported that the correlation was r=0.816 for South Indian females [3], in Zverev YP, study correlation was r=0.871 for males and r=0.815 for the females in Malawian population [15]. According to the most recent researches, Ter Goon TD et al., reported that correlation was r=0.83 in Nigerian adults [5], while Milasinovic R et al., reported that the correlation was r=0.820 in males from northern region in Montenegro [23] and Arifi F et al., reported that the correlation was r=0.794 for males and r=0.766 for females in Kosovan adults [4]. It is found that in Alam MT et al., study, the correlation was r=0.689 for males; r=0.783 for females in eastern Uttar Pradesh [1] and correlation was r=0.806 for males; r=0.866 for females in Shah RK et al., study in Gujarat region, India [16]. Kasunka LGK et al., noted that correlations were r=0.826 and r=0.890 for males and for females respectively in Karnataka, India [30]. Because of the correlation between arm span and stature was high and significant in both Turkish genders, the arm span appears to be a trustworthy anthropometric parameter for predicting the stature in Turkish adults. Although these relationships are similar, the estimation models, which are developed in the Turks, considerably different from other populations. As ethnic, racial and nutritional factors play important role in human growth and development, different formulae have to be applied to different population.
In the current study, when compared with gender, mean arm span and stature in male were more than female and it was statistically significiant (p<0.05). These findings gave similar results to the previous [1,15,17,30]. These results can be elucidated by genetic structure of males. Puberty occurs two years later in males than in females. Therefore, the stature prediction equation developed for females cannot be used for males. Regression equations were developed for stature estimation depending on sex [Table/Fig-8]. The SEEs getting in the current study for arm span was lower than the comparable regression models in the study of Zverev YP [15]. These findings were compatible with results achieved by Supare MS et al., Arifi F et al., Ter Goon TD et al., and Milasinovic R et al., [2,4,5,23]. When the regression equations were evaluated in the randomly selected control group except for the target group, no significant difference was found in both sexes (p<0.001).
Various researches reported that arm span measurements exceeded stature measurements [3,5,24,31]. Ter Goon TD et al., reported that the arm span was 5.8 cm more than stature in Nigerian males (103.3% stature), while for females this difference was merely 4 cm (102.5% stature) [5]. In women aged 20-29 years, the arm span was nearly 2.5 cm more than the stature in South Indian females, which is similar to that noted in the white population [3]. Sah RP et al., reported that the arm span was nearly same as the stature in males, while it was 3.64 cm less than the stature in Nepalese females [22]. In the Arifi F et al., study it was indicated that the arm span was 1.68 cm more than the stature in males (101.0% stature), whereas it was 0.12 cm less than the stature in Kosovan females (99.9% stature) [4]. In the present study, the arm span was 5.91 mm more than the stature in males (100.3% stature), while it was 12.7 mm less than the stature in Turkish females (99.2% stature). The arm span exceeded stature in 51.1% of individuals (n=70). The same relation was observed only 35.0% of individuals (n=48) for females.
Limitation
This research includes the minor sample size, particularly with regards to adults. A more exact prediction of the stature and its estimation to benefit arm span measurements in Turkish adults would necessitate a larger sample with adequate geographical and social heterogeneity or a national examination that evaluates all population. There are several ethnic groups (average 23) in the minority in Turkey (Kurd, Circassian, Azeri, Laz, Armenian, Gagavuz, Arab, Tatar etc.,). This study was conducted only on people of Turks ethnicity who constitute 71% of the population according to 2008 data (United States Center for World Mission-USCWM). The stature estimation models developed in the present study were ground on adult individuals and are not applicable to adolescents.
Conclusion
The current study emphasises that arm span is quite a dependable parameter for estimating the stature and can be used in both sexes. It is applicative in getting age-related loss in stature and in identifying individuals with non-proportional growth and development abnormalities. However, it is a significant parameter medico-legally for identification. This study stands as a practical and reliable models representative for Turkish population.